Cálculo mental – Raíces cuadradas
Score
Nuevo Quiz
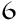
Jugadores
La raíz cuadrada es la operación aritmética fundamental que consiste en hallar un número que, multiplicado por sí mismo, da una cantidad determinada. Se representa con el símbolo «√» y, cuando se aplica, indica el número que, elevado al cuadrado, produce el número inicial.
Por ejemplo, en la operación √16 = 4, 4 es el número que, multiplicado por sí mismo (4 x 4), da 16.
No hay que subestimar la importancia de la raíz cuadrada en el cálculo mental. Se utiliza a diario en muchas situaciones, como la resolución de problemas de geometría, la gestión de las finanzas personales o el análisis de datos estadísticos. Por tanto, saber calcular raíces cuadradas con rapidez y precisión es una habilidad muy valiosa.
En física, por ejemplo, la raíz cuadrada es esencial para determinar valores como la velocidad media, la energía cinética y otras medidas derivadas. Al analizar datos, a menudo es necesario extraer raíces cuadradas para normalizar los resultados o realizar cálculos estadísticos. Del mismo modo, la raíz cuadrada desempeña un papel fundamental en la comprensión de las escalas de medida y las proporciones.
La raíz cuadrada es más que una simple operación matemática; es una herramienta esencial para desenvolverse en muchos aspectos prácticos de la vida cotidiana. Su papel en la aritmética mental es crucial, ya que nos permite tomar decisiones con conocimiento de causa, resolver problemas cotidianos y gestionar los recursos con eficacia.
En matemáticas, y más concretamente en el campo de las raíces cuadradas, el término «raíz» es de especial importancia. Se refiere al número obtenido tras extraer la raíz cuadrada de otro número.
Para ilustrar este concepto, tomemos un ejemplo sencillo: si tenemos el número 25, la raíz cuadrada de 25 es 5, porque 5 multiplicado por sí mismo da 25. En otras palabras, la «raíz» es el número que, multiplicado por sí mismo, da el número inicial.
La «raíz» se aplica no sólo en situaciones sencillas, sino también en contextos más complejos. Por ejemplo, en el caso del área de un cuadrado, si el área es de 36 unidades cuadradas, la longitud de cada lado del cuadrado es la raíz cuadrada de 36, es decir, 6 unidades.
Este concepto es esencial porque proporciona una medida cuantitativa que puede utilizarse en muchas situaciones cotidianas y profesionales, ya sea calculando dimensiones, analizando datos o resolviendo ecuaciones. La «raíz» es, por tanto, una herramienta matemática esencial, que ofrece una perspectiva clara y cuantificable de los resultados derivados de la extracción de raíces cuadradas.
La raíz cuadrada, una operación matemática esencial, está omnipresente en muchas actividades cotidianas y profesionales. La eficacia de esta tarea puede requerir a menudo una ejecución más rápida, especialmente con números complejos. Afortunadamente, existen técnicas para acelerar el proceso manteniendo la precisión.
El método de estimación es un enfoque eficaz que consiste en encontrar dos números entre los que se encuentra la raíz cuadrada y, a continuación, refinar la estimación. Por ejemplo, para hallar la raíz cuadrada de 50, sabes que está entre 7 (7×7=49) y 8 (8×8=64). Afinando, puedes estimar que la raíz cuadrada de 50 es aproximadamente 7,1.
Otra estrategia consiste en utilizar tablas de raíces cuadradas o calculadoras especializadas para hallar las raíces cuadradas de números complejos con rapidez y precisión. Aunque este método es más técnico, resulta eficaz para simplificar los cálculos con números grandes. Por ejemplo, para hallar la raíz cuadrada de 1681, puedes utilizar una calculadora para determinar rápidamente que es igual a 41.
La práctica regular de estas técnicas es esencial para dominarlas. La repetición hace que estos métodos sean intuitivos, lo que facilita el cálculo rápido de raíces cuadradas. Es importante tener en cuenta que el aumento de la velocidad es el resultado de la práctica continua. Sin embargo, la precisión no debe verse comprometida. Es aconsejable comprobar los resultados con regularidad, especialmente durante la fase de aprendizaje.