Calcul Mental – Racines carrées
Score
Nouveau Quiz

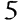
Joueurs
La racine carrée est l’opération arithmétique fondamentale qui consiste à trouver un nombre qui, multiplié par lui-même, donne une quantité spécifique. Elle est représentée par le symbole « √ » et, lorsqu’elle est appliquée, indique le nombre qui, élevé au carré, produit le nombre initial.
Par exemple, dans l’opération √16 = 4, 4 est le nombre qui, multiplié par lui-même (4 x 4), donne 16.
L’importance de la racine carrée dans le calcul mental ne doit pas être sous-estimée. Elle est utilisée quotidiennement dans de nombreuses situations, telles que la résolution de problèmes en géométrie, la gestion des finances personnelles ou encore l’analyse de données statistiques. Savoir calculer les racines carrées rapidement et avec précision est donc une compétence précieuse.
En physique, par exemple, la racine carrée est essentielle pour déterminer des valeurs telles que la vitesse moyenne, l’énergie cinétique et d’autres mesures dérivées. Lors de l’analyse des données, il est souvent nécessaire d’extraire les racines carrées pour normaliser les résultats ou pour effectuer des calculs statistiques. De même, la racine carrée joue un rôle clé dans la compréhension des échelles de mesure et des proportions.
La racine carrée est plus qu’une simple opération mathématique, c’est un outil essentiel pour naviguer dans de nombreux aspects pratiques de la vie quotidienne. Son rôle dans le calcul mental est crucial, car il nous permet de prendre des décisions éclairées, de résoudre des problèmes quotidiens et de gérer efficacement les ressources.
En mathématiques, et plus particulièrement dans le domaine des racines carrées, le terme « racine » revêt une importance particulière. Il désigne le nombre obtenu après avoir extrait la racine carrée d’un autre nombre.
Pour illustrer ce concept, prenons un exemple simple : si vous avez le nombre 25, la racine carrée de 25 est 5, car 5 multiplié par lui-même donne 25. En d’autres termes, la « racine » représente le nombre qui, multiplié par lui-même, donne le nombre initial.
La « racine » s’applique non seulement dans des scénarios simples, mais aussi dans des contextes plus complexes. Par exemple, dans le cas de l’aire d’un carré, si l’aire est de 36 unités carrées, la longueur de chaque côté du carré est la racine carrée de 36, soit 6 unités.
Ce concept est essentiel car il fournit une mesure quantitative qui peut être utilisée dans de nombreuses situations quotidiennes et professionnelles, qu’il s’agisse de calculer des dimensions, d’analyser des données ou de résoudre des équations. La « racine » est donc un outil mathématique essentiel, qui offre une perspective claire et quantifiable sur les résultats dérivés de l’extraction des racines carrées.
La racine carrée, opération mathématique essentielle, est omniprésente dans de nombreuses activités quotidiennes et professionnelles. L’efficacité de cette tâche peut souvent nécessiter une exécution plus rapide, notamment avec des nombres complexes. Heureusement, il existe des techniques permettant d’accélérer la procédure tout en préservant la précision.
La méthode d’estimation est une approche efficace qui consiste à trouver deux nombres entre lesquels se trouve la racine carrée, puis à affiner l’estimation. Par exemple, pour trouver la racine carrée de 50, vous savez qu’elle se trouve entre 7 (7×7=49) et 8 (8×8=64). En affinant, vous pouvez estimer que la racine carrée de 50 est d’environ 7,1.
Une autre stratégie consiste à utiliser des tables de racines carrées ou des calculatrices spécialisées pour trouver rapidement et précisément les racines carrées des nombres complexes. Bien que cette méthode soit plus technique, elle est efficace pour simplifier les calculs impliquant de grands nombres. Par exemple, pour trouver la racine carrée de 1681, vous pouvez utiliser une calculatrice pour déterminer rapidement qu’elle est égale à 41.
La pratique régulière de ces techniques est essentielle à leur maîtrise. La répétition rend ces méthodes intuitives, ce qui facilite le calcul rapide des racines carrées. Il est important de noter que l’augmentation de la vitesse est le résultat d’une pratique continue. La précision ne doit cependant pas être compromise. Il est conseillé de vérifier régulièrement les résultats, surtout pendant la phase d’apprentissage.