Mental arithmetic – Divisions
Score
New Quiz
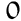
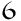
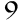

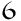
Players
Division is a fundamental arithmetic operation that divides a quantity into equal parts. Symbolized by ÷ or /, it consists in determining how many times a number (the divisor) can be contained in another number (the dividend). For example, in 10 ÷ 2, the result is 5, because 2 fits into 10 5 times.
The history of division goes back to antiquity. The Babylonians and Egyptians were already using division techniques for practical applications such as land division and resource distribution. Over time, the method of division evolved, incorporating tools such as the abacus and sophisticated algorithms, facilitating complex calculations.
Division works differently in different numerical systems. In the binary system, used in computing, division is achieved by successive bit shifts and subtractions, an essential method for processing digital data.
The result of a division is called the quotient. In mathematics, the quotient is the number of equal parts resulting from dividing the dividend by the divisor. For example, for 20 ÷ 4, the quotient is 5. The quotient is a crucial concept not only in elementary arithmetic, but also in algebra and analysis, where it is used to simplify and solve complex equations.
The importance of the quotient is omnipresent in various fields of mathematics. In statistics, for example, the quotient can represent rates or averages, essential elements for data analysis. A case study illustrating the use of the quotient can be found in resource management, where dividing available resources by the number of beneficiaries gives an insight into equitable distribution.
Mastering fast division techniques can considerably improve calculation efficiency.These include the long division method and the use of division tables.Estimate-and-adjust division is also an interesting technique, involving estimating the quotient and then adjusting the remainder.
To practice rapid division, we recommend using a variety of resources such as mental arithmetic games, educational apps and practice exercises. Regular practice improves both the speed and precision of division.
Case studies demonstrate the usefulness of fast division in everyday contexts such as the equitable distribution of tasks or resources, as well as in professional fields requiring fast and accurate calculations.By incorporating these techniques into your routine, you can boost your efficiency and confidence in your mathematical skills.