Mental Arithmetic – Subtractions
Score
New Quiz
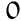
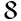
Players
Subtraction is the fundamental arithmetic operation of subtracting one quantity from another. It is represented by the symbol “-” and, when applied, indicates the removal of one number from another to determine what remains.
For example, in the operation 10 – 2 = 8, 2 is removed from 10, leaving 8 as the result.
The importance of subtraction in mental arithmetic cannot be underestimated. It is used daily in a variety of situations, such as managing personal finances, planning time and even allocating resources. Knowing how to subtract quickly and accurately is therefore a valuable skill.
In economics, for example, subtraction is essential to budgeting and avoiding overspending. When you go shopping, you need to subtract the cost of each item from your total budget to avoid spending more than you can afford. Similarly, subtraction plays a key role in the fair distribution of goods, such as food, ensuring that everyone receives a fair share.
Subtraction is more than just a mathematical operation; it’s an essential tool for navigating many practical aspects of everyday life. Its role in mental arithmetic is crucial, enabling us to make informed decisions, solve everyday problems and manage resources efficiently.
In mathematics, and more specifically in the field of subtraction, the term “difference” is of particular importance. It refers to the result obtained after subtracting one number from another.
To illustrate this concept, let’s take a simple example: if you have twelve sweets and four are taken away, the “difference” between the initial number of sweets and the remaining number is eight. In other words, the “difference” represents what’s left or what’s been lost in the subtraction.
The “difference” applies not only in simple scenarios, but also in more complex contexts. For example, in the case of a journey, if you’ve covered 100 kilometers and still have 40 to go, the “difference” of 60 kilometers represents the distance already covered.
This notion is essential because it provides a quantitative measure of change, which can be used in many everyday and professional situations, whether to evaluate distances, adjust budgets or analyze statistical data. The “difference” is therefore an essential mathematical tool, offering a clear, quantifiable perspective on the changes or losses resulting from subtraction.
Subtraction, an essential mathematical operation, is omnipresent in many everyday and professional activities. The efficiency of this task can often require faster execution, especially with complex numbers. Fortunately, there are techniques for speeding up the procedure while preserving accuracy.
The complement method is an effective approach that involves using the “complement” of a number to a neighboring round number, rather than subtracting directly. For example, to subtract 58 from 100, the complement of 58 to 100 is 42, because 58 plus 42 equals 100. Therefore, 100 minus 58 equals 42. This method is particularly useful for financial transactions or measurements where subtraction from a round number is common.
Another strategy is the decomposition method, which involves dividing numbers into smaller units, such as units, tens and hundreds, then subtracting these segments individually. Although this method may seem complex, it is effective in simplifying subtractions involving large numbers. For example, to subtract 168 from 204, we divide and subtract the hundreds, tens and units separately, then combine the results.
Regular practice of these techniques is essential to their mastery. Repetition makes these methods intuitive, which facilitates rapid subtraction. It’s important to note that increasing speed is the result of continuous practice. Accuracy, however, must not be compromised. It is advisable to check results regularly, especially during the learning phase.